广东省燕博园2023届高三年级综合能力测试(CAT)(新高考Ⅰ卷)数学试题答案

广东省燕博园2023届高三年级综合能力测试(CAT)(新高考Ⅰ卷)数学试题答案，目前大联考答案网已经汇总了广东省燕博园2023届高三年级综合能力测试(CAT)(新高考Ⅰ卷)数学试题答案的各科答案和试卷，更多全国100所名校答案请关注本网站。

22.【解析】2,-1(x>0),审题指导令h(x)=lnxx 1a≤0f(x)和g(x)f(x)和g(x[点拨]由于方程的根无法直接求解，考虑通过构造函数，利用导的单调性→最小值的数判断单调性进行求解关系x2 1a>0f(x)和g(x)f(x)则h'(x)=12的单调性g(x)in(x 1)2x( 1)>0,新函数构造新(x)=f(x)和g(x)所以h(x)在(0， ∞)单调递增，又h(1)=0,0 的零点函数g (x)有相同的所以h(x)在(0， ∞)有唯一零点x=1,最小值所以a=1.6分(2)由(1)得f(x).g(x)的直线y=b,曲线(2)由(1)得f(x)=e-x,f(x),g(x)单调区间 y=f(x)和y=g(x三个直线y=b交点的位置的图象g(x)=x-In x(x>0),f(x)在(-∞，0)单调递减，三个交点的横坐标从，三个交点横在(0， ∞)单调递增.y=b左到右成等差数列坐标的关系g(x)在(0,1)单调递减，在x10无012解：(1)f'(x)=e-a,g'(x)=a-(x>0),…1分(1, ∞)单调递增，f(0)=1>0,g(1)=1>0,第22题解图肖a≤0时，f'(x)>0,g'(x)<0,又x→ 时，f(x)→ ∞，g(x)→ 0；[点拨]a的正负影响函数f(x),g(x)的单调性，故需对a分类x→0时，g(x)→ 0；讨论x→-0时f(x)→ ∞，8分即f(x)在R上单调递增，g(x)在(0， ∞)单调递减，则f(x)和g(x)的大致图象如图所示，故f(x),g(x)没有相同的最小值；…2分所以存在唯一x。∈(0,1)，使得f(xo)=g(xo).…9分肖a>0时，令f'(x)=0,得x=lna,令b=f(xo)=g(xo),当x lna时，f'(x)>0,f(x)单调递增，点(x1,f八x)),(x0)),(x28(x2):所以f(x)in=flna)=a-alna.[点拨]根据图象可得当直线y=b经过点(x0,f八x))时，与曲线y=∫(x)和y=g(x)共有三个不同的交点令g'(x)=0,得x=a10分当0 1,且f(x1)=g(xo),即e1-x,=x0-nxo,当时，g(x)>0,g(x)单调递增，所以x,=lno,同理可得x=e0,所以g()=g）=1-h。=1 ha.所以x1 x2=lnxo e0=x。-b x0 b=2xo,…11分4分所以存在直线y=b,与两条曲线y=f(x)和y=g(x)共有三所以a-alna=1 lna,个不同的交点(x1,f(x)),(x0,f(x)),（x2,g(x),且2x1,0,x2成等差数列.12分即lna 1=0,a 1

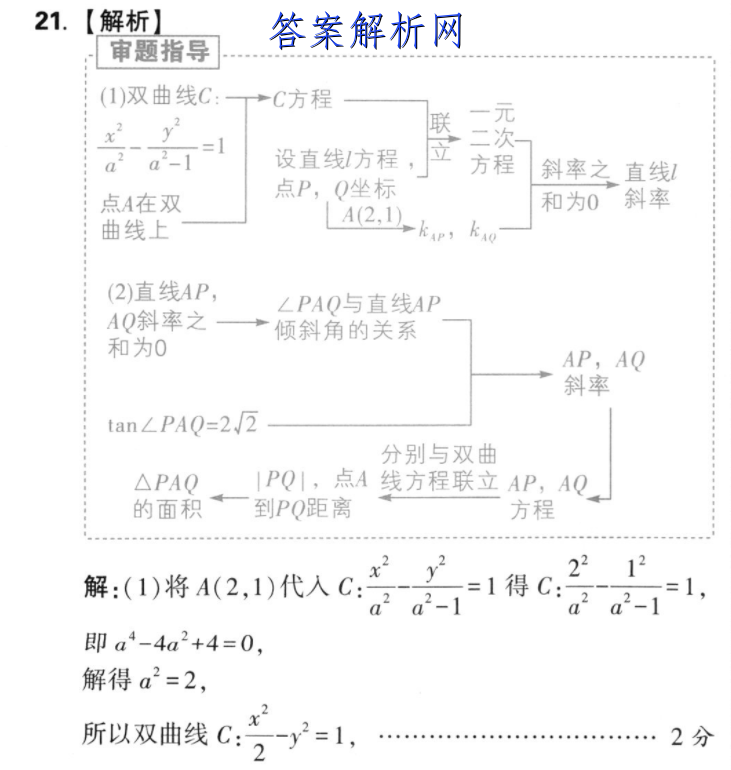
21.【解析】审题指导(1)双曲线C:一→C方程次2a-1设直线方程立方斜率之直线点P,Q坐标点A在双和为0斜率曲线上A(2.D)kr,kao(2)直线AP,∠PAQ与直线APAQ斜率之→倾斜角的关系和为0AP,AQ斜率tan∠PAQ=2J2分别与双曲△PAQ|PQ1,点A线方程联立AP,AQ的面积到PQ距离方程122解：（将421）代人c若1得c号。即a4-4a2 4=0,解得a2=2,所以双曲线Cty2=12分当直线！斜率不存在时，由双曲线对称性可知，直线AP,AQ的斜率之和不可能为0，所以设l:y=kx b,联立2y2=1y=kx b得(2k2-1)x2 4bx 2(b2 1)=0,设P(x1,y1),Q(x2,y2）,4kb则x1 x2=2(b2 1)》2k2-2k2-1由已知△>0，则862-16k2 8>0,因为直线AP,AQ的斜率之和为0，所以kr 6o- x1-2x2-2=0,即(y1-1)(x2-2) (y2-1)·(x1-2)=(kx b-1)(x2-2) (kx2 b-1)(x1-2)=2kx1x22k(x1 x2) (b-1)(x1 x2-4)=0,即4k(8 1) 826 (6-1)(-4h6-8k2 4)2k2-1化简得(k 1)(b 2k-1)=0,解得k=-1或b 2h-1=0,……4分当b 2k-1=0时，b=1-2k,则l:y=kx 1-2k,将A(2,1)代入可得1=2k 1-2k,此时1过点A,不符合题意；…5分当k=-1时，满足条件，所以1的斜率为-1.…6分(2)设直线AP的倾斜角为α，因为直线AP,AQ的斜率之和为0，所以2a ∠PAQ=T或2a=∠PAQ或2a ∠PAQ=2T,又由tan∠PAQ=2,2得tan∠PAQ√222所以kap=tana=tan（T∠PAQ)cot2LPAQ=2.2或kAp=tana=tan22,或kp=tana=tan(T-22又因为双曲线C的渐近线斜率为±？，所以ana=2,所以kp=√2，k0=-√2，则lwy=√2(x-2) 1,40y=-√2(x-2) 1,…8分联立直线P与C得兮y1y=√2(x-2) 1解得x=10-423y=3t联立直线40与C得2少=】y=-√2(x-2) 110 4√2解得x=10 4242 5)】345则0y=-3，310分所以wy= 子，1PQl-5点A到直线PQ的距离d:2211分所以△P0的面积5=分·P01d=分×9x2316212分9